Karger's Algorithm

Karger’s algorithm is a randomized algorithm that solves the Global minimum cut problem.

Terminology

We have 2 new terms, supernodes and superedges
Supernode - A set of vertices
Superedge - For $X,Y$ which are supernodes, the super edge between them is a set which contains all the edges $(x, y)$ such that $x \in X, y \in Y$ .

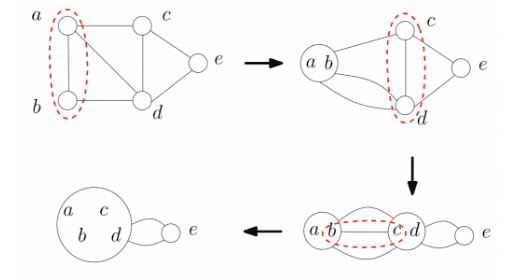
If we had a graph with 4 vertices, and edges

(1, 4), (2, 4), (3, 4)

We could define 2 supernodes

\begin{aligned} X &= \{1, 2, 3\}\\ Y &= \{4\} \end{aligned}

The superedge between $X$ and $Y$ is then defined as

E_{XY} = \{(u, v) | u \in X, v \in Y\}

Algorithm

Karger’s algorithm roughly works as follows -

While the number of supernodes $> 2$ , pick an edge, and merge the two end points of that edge.
Output the remaining superedge when $\#\text{supernodes} = 2$

In this algorithm, we continue to merge supernodes till the the number of supernodes is 2, and then we take a look at the cardinality of the remaining super edge between the superedges, which is a cut for the graph.

Formally,
$\Gamma$ : Set of supernodes
$F$ : Set of superedges
$V(U)$ : nodes in supernode(n)
$\bar v$ : supernode containing $v$

Initially $\Gamma \leftarrow V, F \leftarrow E$
$\text{Merge}(a, b, \Gamma)$
Suppose we want to merge $a, b \in \Gamma$

$x \leftarrow$ new empty supernode
$V(x) \leftarrow V(a) \cup V(b)$
For each $d \in \Gamma \backslash \{a, b\}$ , $E_{dx} \leftarrow E_{da} \cup E_{db}$
$\Gamma \leftarrow (\Gamma \backslash \{a, b\}) \cup \{x\}$

$\text{Karger}(G(V, E))$

Initialize $(\Gamma, E)$
While $|\Gamma| > 2$
1. Pick an edge $e$ from $F$ randomly.
2. $\Gamma \leftarrow \text{Merge}(\bar u, \bar v, \Gamma)$
3. $F \leftarrow F \backslash E_{\bar u, \bar v}$
Return the only superedge

Karger’s algorithm states that the superedge is definitely a cut, and a min cut with some probability.

Claim: If $k$ is the min cut size then $G$ has at least $\frac{kn}{2}$ edges.
We know that if $k$ is the min cut size, then the min degree of any node is $k$ .
If there is some node of degree $k - 1$ or lesser, we could just remove all the edges incident on it to make it disconnected, achieving a min cut less than $k$ .

Now, we can get a lower bound on the number of edges.

\#\text{Edges} \geq \frac{\text{minimum degree} * n}{2}

(The min degree doesn’t have to be exactly $k$ as it could be higher. For example, two densely connected components connected by one edge)

Time Complexity Analysis of Karger’s

We can see that the number of iterations of step 2 in the above algorithm is $\leq n - 2$ as each merge reduces the number of supernodes by $1$ .
Hence, the time complexity is $O(n \cdot (|\text{union}| + |\text{set union}|))$

Correctness Analysis of Karger’s

If we want this algorithm to return the min cut, we need to ensure that in each of the iterations, the end points of an edge from min-cut shouldn’t be contracted/merged.

$E_{i} -$ Event that an edge from the mincut does not get contracted in the $i$ th iteration. $1 \leq i \leq n - 2$
If it’s a connected graph, it’ll need $n - 2$ iterations. If it’s disconnected, then it’ll run in less iterations
For the algorithm to run correctly, all of these events must occur, i.e

\cap_{i=1}^{n-2} E_{i}

We want to find the probability of this occurring.

In this analysis, we’re assuming that we only pick valid edges (i.e edges connecting two different supernodes)

Hence, we want to find

Pr[\cap_{i = 1}^{n - 2} E_{i}] = Pr[E_{1}] \times Pr[E_{2}| E_{1}] \times \dots \times Pr[E_{n-2} | \cap_{j=1}^{n - 3} E_{j}]

Pr[E_{1}] = \frac{|E| - k}{|E|} \geq 1 - \frac{k}{\frac{kn}{2}} = 1 - \frac{2}{n}

Pr[E_2 | E_{1}]= \frac{|F_{1}|- k}{|F_{1}|} \geq 1 - \frac{2}{n - 1}

Now, we claim that

Pr[E_{i}| \cap_{j=1}^{i-1}E_{j}]\geq 1 - \frac{2}{n - (i - 1)}

Say the first iteration $E_{1}$ occurs. After this, the number of nodes in the graph is $n - 1$ , hence the minimum number of edges in the graph is $\frac{k(n - 1)}{2}$ now. Making this generalized, just before $E_{i}$ occurs, there will be $n - (i - 1)$ vertices in the graph, implying that there are at least $\frac{k(n - (i - 1))}{2}$ edges, which leads to

\frac{|E_{j}| - k}{|E_{j}|} = 1 - \frac{2}{n - j + 1}

This would give us

Pr[\cap_{i=1}^{n-2} E_{i}] \geq \prod_{i=1}^{n-2}\left(1 - \frac{2}{n - (i - 1)}\right) = \prod_{i=1}^{n-2} \left(\frac{n - i - 1}{n - i + 1}\right) = \frac{2}{n (n - 1)}

Boosting Success Probability

Say we run a random experiment $s$ times independently, and the probability that it gives the correct answer is $p$ .
Probability that none of the $s$ trials give me the correct answer is $(1 - p)^s$ . Therefore with probability of $1 - (1 - p)^{s}$ , the algorithm gives us the correct answer.

In the case of mincut, $p = \frac{1}{n^{2}}$
Therefore, the probability of all failing is

\leq (1 - p)^ {s}\leq \left(1 - \frac{1}{n^{2}}\right)^{s} \approx e^{-\frac{s}{n^{2}}}

If $s \approx n^{2}$ , then

1 - e^{-1}

Therefore the total time complexity is the time taken to run one instance of Karger’s algorithm, into $s$ , the number of times we run Karger’s.
Hence, we get

T \cdot s = n \cdot |\text{merge}| \cdot n^{2} = n^{3}\cdot |\text{merge}|

Theorem: With probability $1 - e^{-\frac{s}{n^2}}$ and in running time $s \cdot (n \cdot | \text{merge} |)$ min cut can be found.

Weighted Case

We only considered unweighted case, but in flows we usually consider the weighted case. What do we do? We no longer have a bound on the number of edges, but we have a bound on the weight of edges. Therefore the statement

|E| \geq \frac{kn}{2}

doesn’t hold anymore. Hence, we can’t use the same error bound for the weighted flows problem.

Published Feb 2, 2023

Vidit Jain