Clique Finding is NP-Complete

Say we have a formula $\phi$ with $k$ clauses

We create a node for each of $a_i, b_i, c_i$. We then segregate these nodes into groups of three each.

Then, for each node, we connect it to all other nodes outside of its group with an edge, except for those which have a contradictory label, i.e. we won’t create an edge between nodes $x$ and $\bar x$.

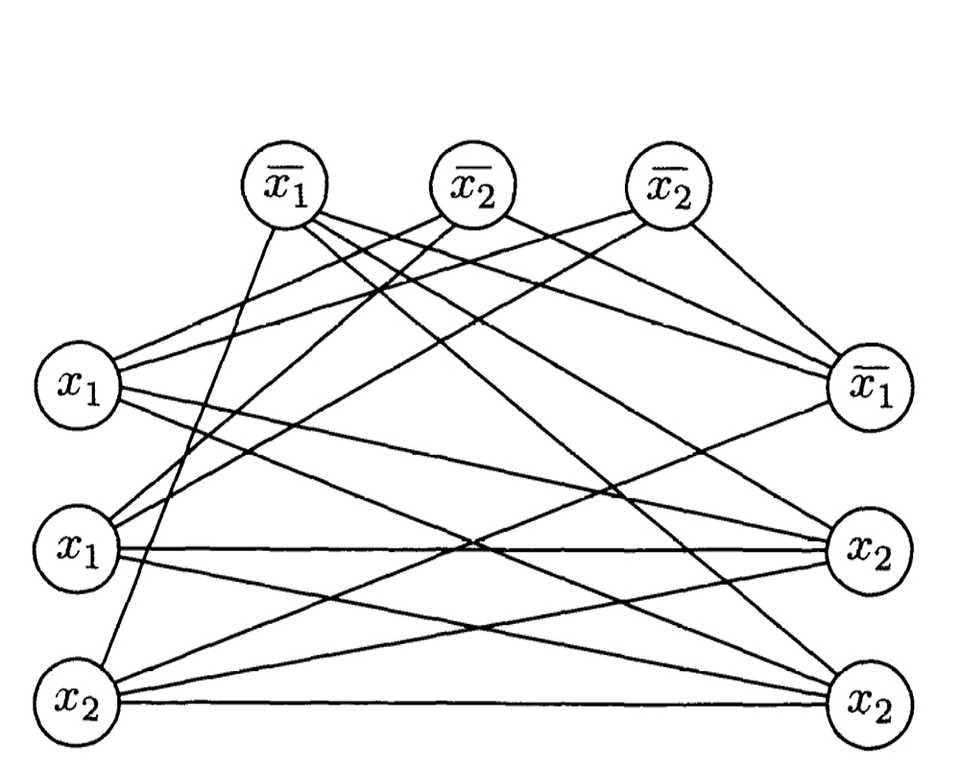
An example of a $3-\text{SAT}$ problem

The graph corresponding to $\phi$ is

Existence of a satisfying assignment implies the existence of a $k$-clique

Now, to satisfy the formula $\phi$, we must find at least one true variable in each group, while making sure they don’t contradict each other.

If we do have a satisfying assignment, then we pick the true term from each group (If there is more than one, then pick any of them).

We know that there would exist an edge between all of them, as they are all in different groups, and a contradiction cannot exist. Hence by construction, the $k$ nodes picked form a clique.

Existence of a $k$ - clique gives us a satisfying assignment

If we have a $k$-clique in the graph, then we know that they must all be from different groups, and we end up picking a node from each group.

We know that a contradiction can’t exist, as a contradiction between nodes would imply the absence of an edge between them, contradicting the fact that the nodes form a clique.

Hence, we can assign all the variables in the clique as $1$ without any contradiction and at least one term in each group would be true.

Hence, we can reduce $3-\text{SAT}$ to an instance of the Clique Finding problem, proving that that the problem is $\text{NP-Complete}$.